自柴油发动机应用于人们的工作与生活之日起, 就以特殊用途存在于各行各业中。高压油管作为发动机工作时的“大动脉”, 承担着为发动机输送高压燃油的艰巨任务, 它连接着高压油泵和喷油机, 是高压油路的重要组成部分。高压油管内的压力变化会导致喷油量出现偏差, 影响发动机的工作效率。高压油管在高压状态下工作时, 喷油器针阀的开、关会使其产生强烈高频振动, 发生漏油事故, 甚至导致油管破裂, 造成经济损失并存在很大的火灾安全隐患[]。因此, 高效控制高压油管的压力变化, 对发动机起着至关重要的作用。
本选题来源于2019年高教杯全国大学生数学建模比赛A题。为了便于解决问题, 提出如下假设:
1) 不考虑燃油在油管内的损失以及管内各种相关摩擦力的影响;
2) 不考虑油管以及喷油器的变形;
3) 不计喷油系统工作期间由压力变化引起的温度变化;
4) 不计喷孔处与外界空气接触面的压力;
5) 正常情况下, 认为燃油的粘度系数、密度为常数;
6) 将高压油管视为等截面圆管, 忽视油管接口处的残余容积对喷射过程的影响;
7) 假设柱塞腔内和高压油管的每一截面上燃油密度均匀一致。
目前, 国内外专家对该问题进行了多方面研究, 刘颖[]建立了恒压变量柱塞泵的仿真模型, 并对其进行动态特性的仿真分析; 刘福水等[]以电控单体泵(EUP)为研究对象, 采用实验和仿真相结合的方法研究凸轮型线与泵端压力间的动态关系; 刘海波[]通过对凸轮曲线廓形的分析, 运用三维建模软件创建高压柱塞泵模型, 得出其刚柔耦合模型, 并对得到的模型进行参数设定、模型验证, 进而进行仿真模拟分析, 得出影响高压柱塞泵内压力的因素; Salvador FJ等[]研究了喷射过程中燃油的内部流动规律, 采用特定的均匀平衡模型进行实验, 用以模拟针阀的实际运动; 郭立新等[]研究了喷油嘴针阀头部结构对喷油嘴内部流动特性的影响规律, 发现针阀头部密封面直径和密封角对喷油嘴内部流动特性的影响相对较大; Elena Fiorese等[]基于整个循环中与流动力相关联的能量估计建立预测模型, 分析了影响柱塞速度的因素; 崔述凯[]分析了影响控制压力参数的主要因素, 提出单向阀产品结构设计的注意事项及检验方法的改进方案; 李龙等[]通过ANSYS Workbench有限元软件对高压油管进行静力学和模态仿真分析, 得出了在静力作用下应力和位移的最大值点, 以及模态振动频率值; 岳进[]建立了凸轮液压柱塞的动力学方程, 研究了柱塞高速运动下的受力特点并计算了柱塞与凸轮的接触应力; 田新伟等[]通过计算流体力学仿真获取高压油管内部燃油脉冲压力, 并通过建立高压油管流固耦合模型, 进行振动特性仿真分析。
1 研究思路
对于单向阀开启时长的控制问题, 首先基于燃油喷射的基本过程, 分析影响燃油压力变化的因素, 通过对喷油系统的简化, 建立基于燃油进入和喷出的间歇性工作过程的时长关系模型, 根据赛题所给喷油速率图像确定流量与压力的关系; 然后, 通过对赛题附件3所提供压力和弹性模量的数据预处理, 得到压力和弹性模量拟合图, 确定不同压力情况下的密度值, 然后在油管内压力稳定的条件下引入连续性方程中的质量守恒进行单向阀开启时长问题的求解; 最后, 在理想化的动态平衡条件下对所建立的模型进行误差分析。为确定压力稳定条件下凸轮的角速度, 首先通过针阀底端和喷孔面积求出燃油喷出量; 然后得出高压油泵凸轮驱动柱塞的升程, 再结合赛题所给附件1中极角与极径数据信息, 得出凸轮边缘曲线和基圆曲线; 最后结合针阀升程周期图像, 求得高压油管内压力尽量稳定在100 MPa时凸轮的角速度。
2 模型的建立与求解2.1 单向阀的开关时长
某高压燃油系统的工作原理如所示。
图 1

图 1 高压油管示意图
燃油经过高压油泵从A处进入高压油管, 再由喷口B喷出。高压油管中燃油的进入和喷出是间歇性工作的, 当油管内压力达到稳定时, 进出油管的油量达到动态平衡。赛题所给喷油速率示意, 可建立一个周期内的喷油量QB与时间t的方程如下:
图 2
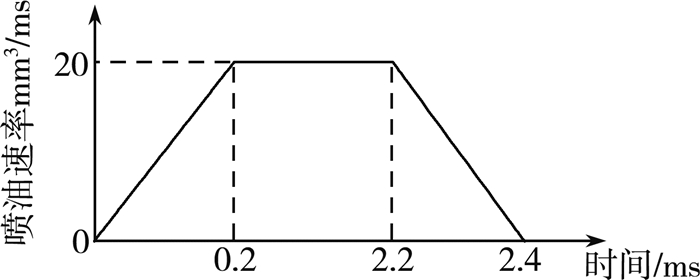
图 2 喷油速率示意图
$Q_{B}=left{begin{array}{ll}int_{0}^{t} 100 t d t & , 0
(1)
高压油管内的流量受到管道内部各种物理量的影响, 而最主要的影响来自于压力P。随着压力的变化, 高压油管进出口燃油的密度ρ发生变化, 从而流量也随之发生变化。
1) 首先由赛题提供的高压油管内的流量公式:
$Q=C S sqrt{frac{2 Delta P}{rho}}$
(2)
其中, C=0.85为流量系数, S为小孔的截面面积(mm2), ΔP为小孔两边的压力差(MPa), 结合公式(2.2)可确定进油管A处燃油的质量变化为:
$d_{m_{A}}=rho_{A} Q_{A} d t=0.85 S sqrt{2 rho_{A}left(P_{A}-Pright)} d t$
(3)
那么喷油点B处的燃油质量变化为:
$d_{m_{B}}=rho_{B} Q_{B} d t$
(4)
为进一步确定P/ρ的变化规律, 可知燃油的压力变化量与密度变化量成正比, 比例系数为E/ρ, 当压力为100 MPa时, 燃油的密度为0.850 mg/mm3, E为弹性模量, 可得微分方程:
$frac{d P}{d rho}=frac{E(p)}{rho}$
(5)
根据所提供的关于压力和弹性模量的数据, 对其进行拟合运算, 结果如所示:
图 3
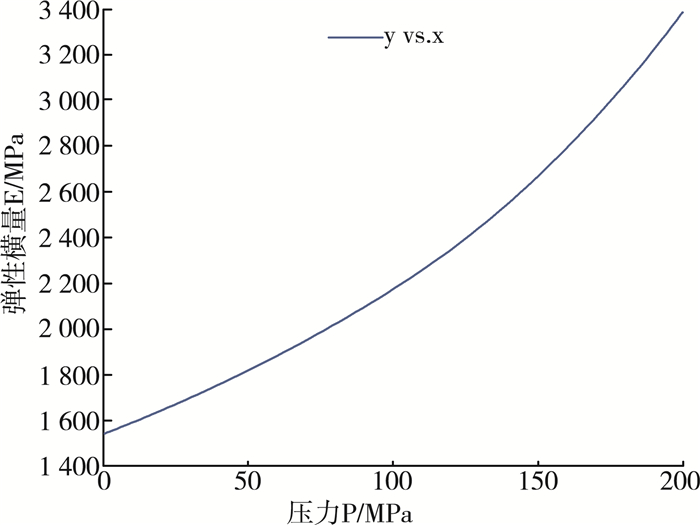
图 3 压力和弹性模量拟合图
由可知, 弹性模量随着压力的增大而增大, 其函数关系式为:
$E=0.03 P^{2}+3 P+1.6 times 10^{3}$
(6)
在此基础上, 结合式(5)和的拟合曲线变化关系得出弹性模量和压力变化量与密度变化量的动态关系。经过对式(5)两边同时积分并代入所给初值条件, 求出系数E/ρ为0.8, 并有:
$rho=0.8 int frac{d P}{E(P)}$
(7)
以此关系式来确定不同压力情况下密度的值, 以160 MPa的燃油密度为例, 可求出其密度ρ=1.09 g/ml。
2) 由赛题可知, 油管进出口油量与时间变化量存在一定的关系, 且油管中各种条件变化都可引起燃油的流动变化, 因此单向阀和油管喷嘴的燃油之间满足连续性关系。不考虑油管以及喷油器体的变形, 那么压力的变化主要引起燃油密度的改变, 从而引起燃油质量的改变。因此, 在油管体积V一定的情况下, 管内燃油质量的变化量Δm满足连续性方程中的质量守恒关系:
$Delta m=d m_{A}-d m_{B}=rho_{text {内 }} V$
(8)
根据所给条件算出
V=0.850×π×52×500=39 250 mg/mm3
ρ内为油管内燃油密度, 等同于喷油处密度ρB。把式(2.3)和(2.4)代入式(2.8)中, 得出油管内油量变化关系式为:
$frac{V d P}{left(0.85 S sqrt{ 2 rho_{A}left(P_{A}-Pright)-rho_{B} Q_{B}}right) d t}=frac{E}{rho_{text {内 }}}$
(9)
对上式进行分离变量并积分, 得到:
$Delta t=int frac{rho_{text {内 }} V}{Eleft(0.85 S sqrt{ 2 rho_{A}left(P_{A}-Pright)}-rho_{B} Q_{B}right)} d P$
(10)
此式是关于时间随压力变化的函数表达式。计算开启时长时, 先计算一个周期内的, 后面的周期都是同等情况。先根据式(6)求出相应的密度, 再结合式(1)中喷油量QB(mm3/s)随时间t在一个单位周期的变化量,以此来根据式(2)确定P在一个周期内的积分范围, 最终来确定单向阀的开启时长Δt。当压力发生变化时, 同样可用此式进行求解。
代入相应数值即可求得单向阀的开启时长Δt。
1) 稳定在100 MPa时, 这时ΔP=60 MPa, 求出Δt=0.31 ms。
2) 稳定在150 MPa时, 这时ΔP=10 MPa, 求得经2 s调整达到150 MPa, 根据计算求出Δt=69.85 ms; 经5 s调整达到150 MPa, 根据计算求出Δt=50.98 ms; 经10 s调整达到150 MPa, 根据计算求出Δt=44.68 ms。
为检验模型的准确性, 假设在理想状态下, 要保持高压油管压力稳定, 则要求高压油管内的进油量等于喷油量, 达到动态平衡状态(相对静止)。根据这一等量条件, 对单向阀的开启时长进行求解。以1 s为时间单位(即1 000 ms)进行计算, 把这1 s分割成n个小段, 每个小段内单向阀开启时长为Δt(ms), 关闭时长为10 ms, 如所示:
图 4
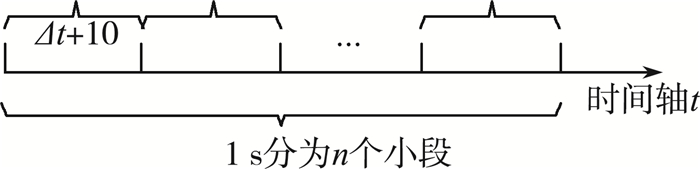
图 4 单向阀时间间隔示意图
单向阀每打开一次关闭10 ms, n个时间间隔关闭10 nms, 根据赛题所给的喷油速率示意, 求出图中平面图形的面积, 可得一个周期喷油量为QB, i(mm3/ms)(i=1, 2…, 10表示周期数), 则一个周期总油量为QB, i=44(mm3/ms)在时间相等和进油量与出油量相等两个方面列出方程组如下:
$left{begin{array}{l}n Delta t+10 n=1000 \Delta t Q_{B, i} n=440end{array}right.$
(11)
求出高压油管内压力稳定在100 MPa时, Δt=0.299 s, 与模型求得的时间Δt=0.31 ms相比, 误差为3.5%, 在波动范围0~5%内。
2.2 凸轮角速度的确定
1) 在实际工作过程中, 高压油管进口处的燃油来自高压油泵的柱塞腔出口, 喷油由喷油嘴的针阀控制, 高压油泵柱塞的压油过程如所示。
图 5

图 5 高压油管实际工作过程示意图
凸轮驱动柱塞上下运动, 压缩柱塞腔内的燃油, 当柱塞腔内的压力大于高压油管内的压力时, 柱塞腔与高压油管连接的单向阀开启, 燃油进入高压油管内。先从喷油嘴处考虑, 当针阀升程大于0时, 燃油才能喷出, 但是喷油孔的大小是一定的, 当针阀升程较大时, 针阀底端平面的漏油量大于喷孔出油量; 当针阀升程较小时, 针阀底端平面的漏油量少于喷孔出油量, 很明显当针阀底端平面的漏油量等于喷孔出油量时, 处于平衡阶段, 如所示。
图 6
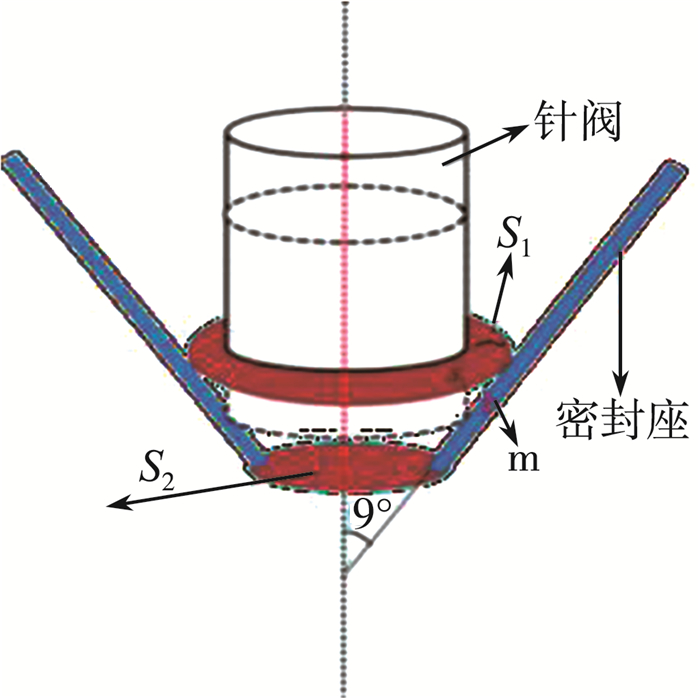
图 6 平衡状态下的喷嘴截面图
针阀底部截面面积S即为针阀底端面积S1与喷孔面积S2之和, 表示为
$S_{1}+S_{2}=S$
(12)
则当S1=S2时, 达到平衡, 对应的直径d1=3.9 mm。
2) 由赛题知, 密封座为半角9°的圆锥, 喷孔直径d2为1.4 mm, 因此在平衡状态下, 利用正切函数计算出该状态下针阀底端离锥顶距离h1, 以及喷孔离锥顶距离h2。
$left{begin{array}{l}h_{1}=frac{d_{1}}{2 tan 9^{circ}} \h_{2}=frac{d_{2}}{2 tan 9^{circ}}end{array}right.$
(13)
高度差h(h1与h2的差), 即为平衡状态下针阀的升程。可求出平衡状态下喷出油量体积V出, 进而求得油量m出=ρV出=155.2 mg。
3) 再从高压油管进出油量相等的条件出发, 则有
$m_{text {进 }}=m_{text {出 }}=155.2 mathrm{mg}$
(14)
燃油进入高压油管中的体积在单位时间内是不定的, 可借助柱塞腔的高度进行转换,
$m_{text {进 }}=rho_{text {进 }} S_{text {进 }} H$
(15)
S进为柱塞腔内的底面积, H为腔内燃油的高度, 求出喷进油量在柱塞腔内的高度H=7.26 mm。赛题中指出在柱塞运动的上下止点处并不能完全将油喷出, 柱塞腔内残余燃油容积为V′=20 mm3, 而残余容积也占距一定高度H′=1.02 mm。则柱塞上升的高度H1为:
$H_{1}=H-H^{prime}=6.24 mathrm{ mm}$
(16)
4) 凸轮的边缘曲线对喷油过程有着重要影响, 凸轮推动柱塞的运动根据凸轮边缘曲线的不同而不同, 而柱塞的运动决定了进入高压油管的燃油量, 又由于凸轮边缘曲线决定着凸轮的角速度, 也就是说, 凸轮的角速度决定着喷嘴的喷油过程。依据赛题附件1中极角与极径数据信息, 利用Matlab软件得出凸轮边缘曲线以及基圆曲线如所示。
图 7
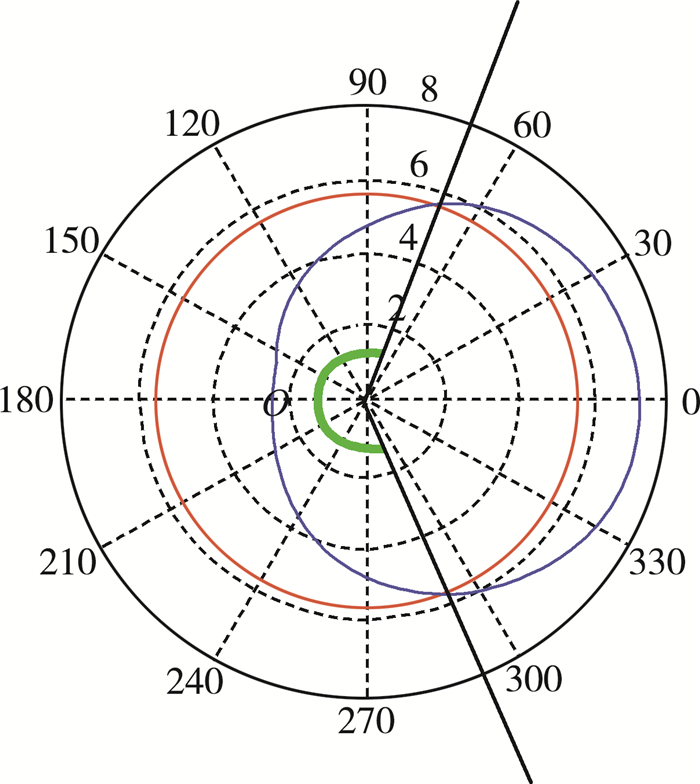
图 7 凸轮边缘曲线及基圆曲线
的红线表示以柱塞上升的高度作为凸轮的基圆半径, 以极点为圆心所作的圆, 根据凸轮边缘曲线及基圆曲线, 利用图解法得出凸轮的偏心距e=12.7 cm, 所画圆与凸轮的线型轮廓重合的部分, 取两交点分别连接极点得到两条极线, 求出其所围成的极角θ。赛题中附件2所给为针阀升程与时间的一个周期的变化关系, 通过Matlab软件得到一个运动周期T内的针阀升程图像, 如所示。
图 8
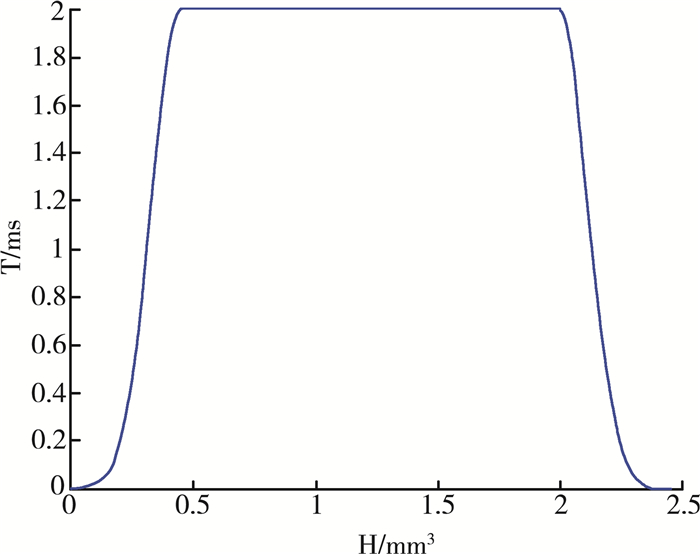
图 8 一个周期内针阀的升程变化
设凸轮以等角速度转动, 则凸轮的转动速度v1为常数, 且等于柱塞上升的速度, 则
$v_{1}=frac{H_{1}}{T}$
(17)
凸轮角速度公式为
$omega=frac{v_{1}}{e sin (pi-theta)}$
(18)
根据式(17)和式(18), 求得在高压油管压力稳定在100 MPa时的凸轮角速度ω=3.079 rad/ms。
3 结论
基于动态平衡的高压油管的压力控制问题, 针对单向阀开启时长和凸轮角速度的确定问题展开研究, 得到以下结论:1)在进入高压油管的燃油由供油入口处的单向阀控制, 喷出的燃油由喷油嘴控制的情况下, 为了使高压油管内的压力分别尽量稳定在100 MPa和150 MPa, 求得单向阀开启的时间长度, 从而精确控制喷油量, 提高发动机的工作效率。2)当进入高压油管的燃油来自于高压油泵的柱塞腔出口, 喷出的燃油由喷油嘴的针阀控制时, 为了使高压油管内的压力尽量稳定在100 MPa, 求得驱动柱塞上下运动的凸轮角速度。
建立的模型具有坚实可靠的数据基础, 且与实际情况紧密结合, 突出了压力有效控制的重要性, 并充分考虑物理学原理, 使模型具有很好的通用性和推广性。
原文链接:http://www.wzcl.net/kuajing/7899.html,转载请注明出处~~~
免责声明
本站提供的一切软件、教程和内容信息仅限用于学习和研究目的;不得将上述内容用于商业或者非法用途,否则,一切后果请用户自负。本站信息来自网络,版权争议与本站无关。您必须在下载后的24个小时之内,从您的电脑或手机中彻底删除上述内容。如果您喜欢该程序,请支持正版,购买注册,得到更好的正版服务。如有侵权请邮件与我们联系处理。敬请谅解!



评论0